Mudanças entre as edições de "Raquels:webquest2"
| Linha 56: | Linha 56: | ||
# Começarei a aula construindo os gráficos do seno e do cosseno utilizando o Geogebra. | # Começarei a aula construindo os gráficos do seno e do cosseno utilizando o Geogebra. | ||
# trabalhar as situações a seguir, pedindo aos alunos que insiram os dados no Geogebra observando as mudanças no gráfico: | # trabalhar as situações a seguir, pedindo aos alunos que insiram os dados no Geogebra observando as mudanças no gráfico: | ||
| − | 'Situação 1': Consideremos a função seno cuja expressão é dada por y=f1(x)=sen(x)+k, onde k é uma constante real. Qual a ação da constante k no gráfico desta nova função quando comparado ao gráfico da função inicial y=sen(x)? | + | '''Situação 1''': Consideremos a função seno cuja expressão é dada por y=f1(x)=sen(x)+k, onde k é uma constante real. Qual a ação da constante k no gráfico desta nova função quando comparado ao gráfico da função inicial y=sen(x)? |
Edição das 19h54min de 19 de junho de 2016
Plano de Aula utilizando Geogebra:
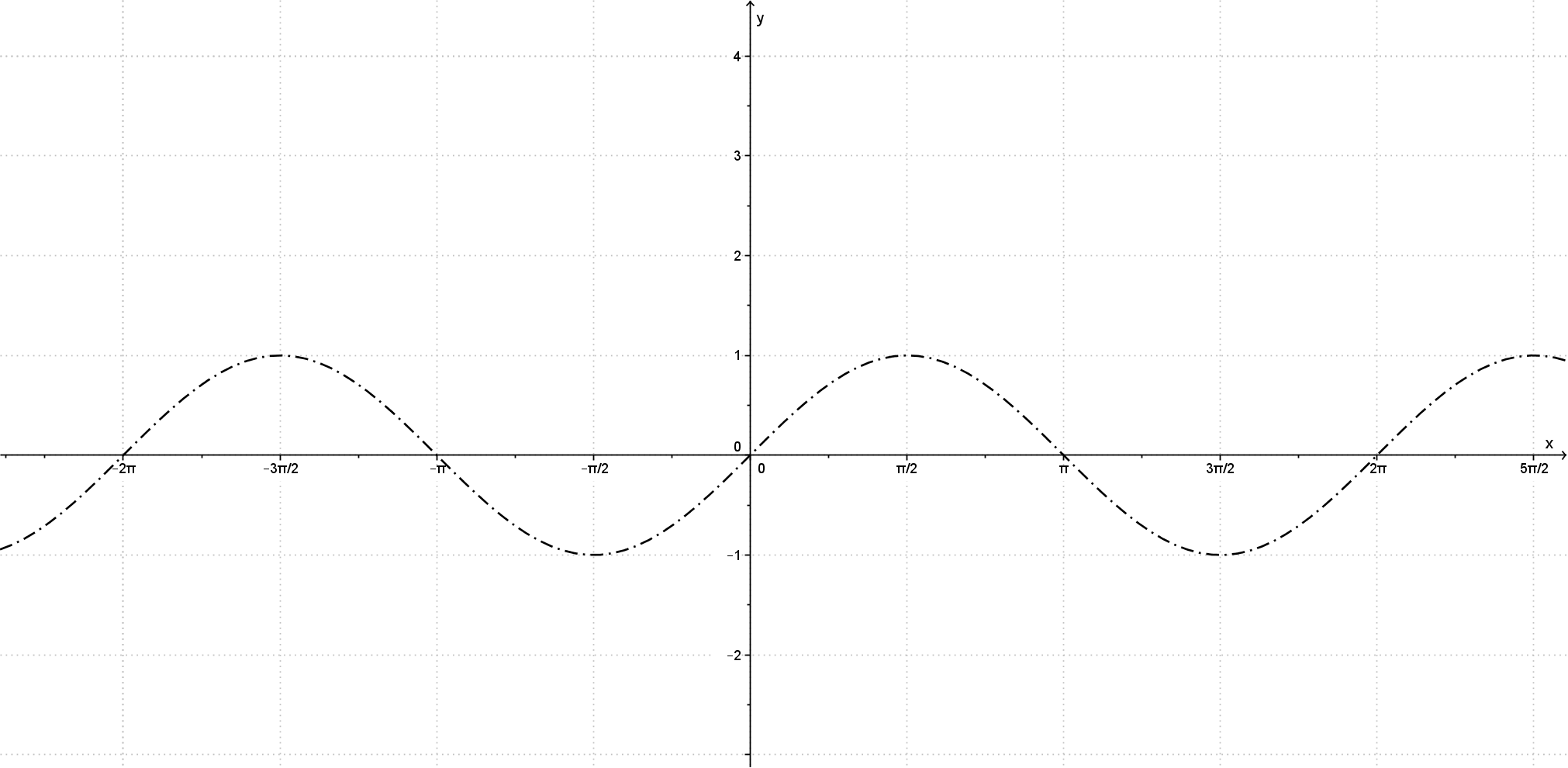
Começarei a aula apresentando o gráfico do seno e do cosseno utilizando o Geogebra.
Depois irei trabalhar as situações a seguir, pedindo aos alunos que pensem em como ficará o gráfico e desenhando um esboço no gráfico cartesiano:
Situação 1: Consideremos a função seno cuja expressão é dada por y=f1(x)=sen(x)+k, onde k é uma constante real. Qual a ação da constante k no gráfico desta nova função quando comparado ao gráfico da função inicial y=sen(x)?
Fazer uma tabela e aplicar, supondo k=1
| x | sen(x) | sen(x)+k |
| 0 | 0 | 1 |
| 90º ou π | 1 | 2 |
| 270º ou 3π/2 | -1 | 0 |
Observar que o gráfico se altera na imagem
Situação 2: Vejamos agora a função seno cuja expressão é dada por y=f(x)=sen(x+k), onde k é uma constante real. Qual a ação da constante k no gráfico desta nova função quando comparado ao gráfico da função inicial y=sen(x)?
Fazer uma tabela e aplicar, supondo k=π/2
| x | sen(x) | (x+k) | sen(x+k) |
| 0 | 0 | π/2 | 1 |
| π/2 | 1 | π | -1 |
| π | 0 | 3π/2 | 0 |
| 3π/2 | -1 | 2π | 1 |
Observar que o gráfico se altera no domínio.
Introdução
Plano de aula utilizando o Geogebra:
- Alunos em duplas para discutir as alterações sofridas nos gráficos que será visualizado dentro do programa Geogebra;
- Tempo necessário: 3 períodos de aula;
- Objetivo: Entender as alterações dos gráficos do seno e cosseno para realização de exercícios da prova de vestibular da UFRGS.
Procedimento
- Começarei a aula construindo os gráficos do seno e do cosseno utilizando o Geogebra.
- trabalhar as situações a seguir, pedindo aos alunos que insiram os dados no Geogebra observando as mudanças no gráfico:
Situação 1: Consideremos a função seno cuja expressão é dada por y=f1(x)=sen(x)+k, onde k é uma constante real. Qual a ação da constante k no gráfico desta nova função quando comparado ao gráfico da função inicial y=sen(x)?
Resultado
Então podemos concluir que a raiz quadrada de 73 é aproximadamente 8,544, pois 8,544*8,544=72,9999