Mudanças entre as edições de "Rebecac:webquest2"
(Criou página com '200px|thumb|left|Gif animado 200px|thumb|left|Ângulos internos de um triângulo Construir três ponto...') |
m |
||
| (Uma revisão intermediária pelo mesmo usuário não está sendo mostrada) | |||
| Linha 1: | Linha 1: | ||
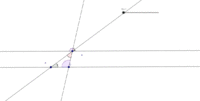
[[Arquivo:Ângulos triângulo.gif|200px|thumb|left|Gif animado]] | [[Arquivo:Ângulos triângulo.gif|200px|thumb|left|Gif animado]] | ||
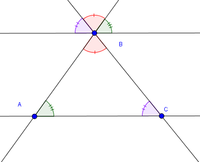
[[Arquivo:Triângulo ângulos.png|200px|thumb|left|Ângulos internos de um triângulo]] | [[Arquivo:Triângulo ângulos.png|200px|thumb|left|Ângulos internos de um triângulo]] | ||
| + | |||
| + | *'''Atividade:''' | ||
| + | |||
| + | '''Demonstração da soma dos ângulos internos de um triângulo''' | ||
Construir três pontos A, B e C não colineares | Construir três pontos A, B e C não colineares | ||
| Linha 17: | Linha 21: | ||
| − | Traçar o | + | Traçar o ângulo ABC |
| + | |||
| + | |||
| + | Traçar o ângulo BCA | ||
| + | |||
| + | |||
| + | Traçar o ângulo CAB | ||
| + | |||
| + | |||
| + | Solicitar que os alunos marquem os ângulos presentes na figura, formados pelas retas traçadas. Questionar quais destes ângulos são semelhantes, utilizando para isto conceitos de semelhanças de triângulos, teorema de Tales ou ângulos opostos pelo vértice. | ||
| − | + | A ideia é que os alunos percebam que a soma dos ângulos internos de um triângulo forma 180 graus, e como é possível demonstrar este fato utilizando os conceitos citados acima. | |
| − | + | '''Tarefa desafio:''' | |
| + | Solicitar que os alunos tentem utilizar um raciocínio semelhante para determinar a soma dos ângulos internos de um quadrado. | ||
Edição atual tal como às 19h20min de 8 de maio de 2016
- Atividade:
Demonstração da soma dos ângulos internos de um triângulo
Construir três pontos A, B e C não colineares
Traçar uma reta passando por AB
Traçar uma reta passando por BC
Traçar uma reta passando por CA
Traçar uma reta paralela ao segmento CA passando pelo ponto B
Traçar o ângulo ABC
Traçar o ângulo BCA
Traçar o ângulo CAB
Solicitar que os alunos marquem os ângulos presentes na figura, formados pelas retas traçadas. Questionar quais destes ângulos são semelhantes, utilizando para isto conceitos de semelhanças de triângulos, teorema de Tales ou ângulos opostos pelo vértice.
A ideia é que os alunos percebam que a soma dos ângulos internos de um triângulo forma 180 graus, e como é possível demonstrar este fato utilizando os conceitos citados acima.
Tarefa desafio:
Solicitar que os alunos tentem utilizar um raciocínio semelhante para determinar a soma dos ângulos internos de um quadrado.